>対角線の長さが6cmの立方体はどう求めたらいいんですか? x2条x2条=6の2条 で一辺求めればいいのですか? 立方体の対角線の長さはちょっとトリッキーで、 底面の対角線、高さをその他の2辺とした直角三角形で三平方の定理を使うよ。 詳しくは「立方体の対角線の求め方」を読ん2個の頂点を結ぶ線分の本数 6c2=15 本から、辺の数を引いたら、対角線の本数が出ます。(156=9 ) 答えは、9本 間違えていたら、ごめんなさい!正10角形の1つの内角の大きさ =10角形の内角の和÷10 =1440÷10 =144度 まとめ 正 角形の角度の問題ではほとんどの場合で内角の和の公式を使います。覚えておきましょう。 問題と解説を詳しく見る 中学受験4年 72 多角形と角度

正多角形の対角線
正10角形 対角線
正10角形 対角線-正18 角形の対角線の交点について 友田勝久 はじめに 正18 角形の対角線をすべて引くと,多く の交点において,3 本以上の対角線が交わっ ていることがわかる。4 本や5 本の対角線が 1 点で交わることも多く観察される。2.正12 角形の対角線の性質について調べてみよう。 3 本以上の対角線が交わって いる点は図のように3 種類に分 類できる。 緑の点 赤の点 青の点 このうち、青の点で3 本の対角 線が交わることを説明してみよ う。 〔ヒント〕 正12 角形の辺ac に対する中



十一角形 Wikipedia
最初に,プリントにある正12 角形にm=2k の場合の対角線を描いて,m=ak の意味を 理解できるようにした。図の確認は,生徒機PC 間のモニターにプリントを映して行った。 「正n角形対角線変化版_1gps」で,nを12 から30→60→1 と増やし,対角線の本数ということにします。ただし,正5 2 角形,つまり星形正五角形は除きます。 やみくもに作図しても仕方がありませんから, まずは,正五角形のことについてよく調べてみましょう。 問題1 正五角形abcdeにおいて、 対角線beを引くことでできる十角形の場合,一つの頂点から引ける対角線の本数は 10-3=7(本). 自分自身と両隣には対角線を引けませんが,それ以外の7つの頂点には対角線を引ける. 頂点は全部で10個あるので,7x10=70(本). ただし,それだと同じ対角線を二度ずつ数えているので2で割って 70÷2=35(本). 35本が答えになる. task 1年以上前
(解)正10 角形をabcdefghij とし,中心をo とする。 10 個の頂点の中から4 点を選び,その4 点を頂点に持つ四角形の対角線 は2 本で交点は1 個できる。いろいろな立体の問題 第2節 立体の回転体の体積(その5) 次に正12面体の回転体の体積を求めよう.一見難しそうであるが,空間座標上における正12面体の頂点の座標を利用すると 比較的簡単に求めることができる.なお,正5角形,正12面体の諸量の求め方は 第4節正多面体の体積 にあるので正5角形・正7角形とトレミーの定理(その3) 正多角形 Wikipedia;
(対角線の長さ) = (1辺の長さ) × 2 なので、 10 2 c m が対角線の長さになります。 2 (二乗して2になる数)はだいたい 1414 なので、おおよその長さは 10 × 1414 = 1414 c m と求めることができます。対角線の長さは、 対角線の長さ = = 辺の長さ ×√2 × 2 = 10×√2 = 10 × 2 = 10√2 = 10 2 ∴ ∴ 対角線の長さ = 10√2 = 10 2 となります。 このように、正方形の対角線の長さは、辺の長さに √2 2 をかけるだけで求められます。 √2 2 をかけるだけなので簡単ですね正多面体 プラトンの正多面体とも呼ばれる. 同じ大きさの正多角形(正p角形)で囲まれ、 どの頂点にも同数個(q個)の正多角形が集まって、 同じ形をしている立体を正多面体という. このときp≧3, q≧3 である. (p, q) をシュレーフリーの記号という.




多角形と正多角形 Youtube



Idan Tal
正n角形とその対角線 すべてについては、1つの頂点から出ている対角線の数が奇数となる場合、すなわちnが4以上の偶数のときAのグループ、1つの頂点から出ている対角線の数が偶数となる場合、すなわちnが5以上の奇数のとき B 前記正十二角形燃料棒配列のうちの所定の正十二角形燃料棒配列は、その正十二角形の頂点の対角線の交点の位置に一本のウォーターロッド 子供の中学校時の作品(多角形対角線)を Inkscape でまねてみました。 正多角形対角線図を描く 1.正多角形を描く 画面左側の「ツールボックス」から「星形/多角形ツール」を選び、19角形を描く (ガイド線を入れているがガイド線は特に必要では正十二角形の対角線の長さ・面積 正十二角形の 辺の長さを ,外接円の半径を ,内接円の半径を とする。 つの辺たとえば に対する弧 の中心角は ,円周角は , 正十二角形の内角は ,外角は である。




十一角形 Wikipedia




高校数学 正十二角形の周長と面積 多角形の求積の原則 受験の月
基本的なので答えのみ. 全3角形数 n C 3 2辺共有 n 1辺だけ共有 n (n4) 3 直角3角形の個数 奇数の場合 0 (∵ 正n角形を真っ2つにする対角線が引けません.) 偶数の場合 対角線 A 0 A n/2 と対角線 A n/2 A 0 が同じですが 1方の領域のみを考える事でダブりを 正n角形の対角線をすべて引いたとき、内部に別の正n角形ができる。 元の正n角形と内部の正n角形の相似比 r は、 r = sin θ 2 cos θ で与えられる。 ただし、ここで、 θ = π n とした正方形の対角線は141Lです。 Lは正方形の辺の長さです。 正方形は全ての辺が等しく、隣り合う辺のなす角度が直角です。 正方形に対角線を引くとき2つの三角形ができます。 この三角形の斜辺をピタゴラスの定理で算定すると141Lが算定できます。 今回



正多角形の対角線



正多角形の内接円の半径 倭算数理研究所
どうやら奇数角形のときには真ん中に子供ができる ことがいえそうです。 美しい!と褒めたら、翌日彼女は何と! 正36角形の対角線を引いてきたのです! ↓ (もちろん生徒の手書きです。実物は直径10センチほど) これを見て、皆さんどう思いますか ところが、一本の対角線は、ある頂点Aから他の頂点Zへの対角線として数えられたと同時に、頂点Zから頂点Aへの対角線としても数えられています。 つまり、一本の対角線が二度カウントされた事になりますので、実際の数はその半分になります。 したがって、n角形の対角線の数Xは、X=n(n3)/2 となります。 これは、一つの頂点から引ける対角線の数(n3)が頂点 (10−3)×10÷2=35で、正十角形の対角線の本数は35本ということがわかります。 このように、正n角形の対角線の本数は(n−3)×n÷2で出すことができるのです。 ぜひ覚えておいてくださいね。 (963文字)正多角形の内角の和っていくつ?? 正多角形の内角をぜーんぶ足したら



1




十二角形 Wikipedia
A そこで一つの正三角形の頂点をそれぞれA、B、Cとし、辺BCに 垂 直二等分線を引く。垂直二等分線と辺BCの交点をDとする。そうす れば、図のようなΔABDができる。三平方の定理と使って線分AD の長さを求めると、 B D C X²=11辺の長さが10の正5角形の対角線の長さである。1辺の長さが2の正5角形の対角線 の長さは、1+ なので、 AB=5+5 となる。 (終) (コメント) 高校生ならば、この問題は真っ先に余弦定理を思いつくだろうが、計算がとても 正n角形の対角線の数を求める公式を次の1から3の手順で導け。ただし、nは4以上の整数とする。 1正n角形のn個の頂点の中から2個を選ぶ選び方の総数を求める 2隣り合う2つの頂点を選ぶときの選び方の総数を求める 3①で求めた総数をひく 大至急お願いいたしますm(__)m



その1 驚き 正n角形の1頂点から他の頂点までの全線分の積はn



正多角形の対角線
正十角形 対角線 (10−3)×10÷2=35で、正十角形の対角線の本数は35本ということがわかります。 このように、正n角形の対角線の本数は (n−3)×n÷2で出すことができるのです。正n角形の対角線の交点の個数は、 n C 4 + (-5n 3 +45n 2 -70n+24)/24・δ 2 (n)-(3n/2)・δ 4 (n) +(-45n 2 +262n)/6・δ 6 (n)+42n・δ 12 (n)+60n・δ 18 (n)正八角形の対角線の数を求めなさい。 式 答え 1つの外角の大きさが°であるのは正何角形か。 式 答え 内角の和が °であるのは、正何角形か。 式 答え 内角の和が °であるのは、正何角形か。 式 答え 1800 ③ ④ ⑤ 1440 ⑥ no1 ② 10分 /6 ①




中2の数学の図形の問題です 答えは 形 正十二角形 対角線の数 54本です Clear




正多角形の対角線
n角形の対角線の数は、n*(n3)/2本となり、種類ごとに分けると1種類あたりn/2本(円の中心を通るもの)またはn*2/2本(それ以外)となります。 以上から、短い順に 6角形:6,3の計9 7角形:7,7の計14 8角形:8,8,4の計 9角形:9,9,9の計27 10角形:10,10,10,5の計35正 7 角形 対角線 正十角形の対角線は何本ありますか?説明つきでお願いします 正7角形のある性質 xsrvjp;正7角形の対角線の長さに関する問題で 1/x1/yを求めていますが その逆数を求めると単位の次元が合うのでおもしろいかなとおもいました。 1/(1/x1/y)=a となり(a=正7角形の1辺の長さとする)すると次のように表現できる。




ポテト一郎 個人的には 正七角形は正多角形の中で1番好きです



フェリス女学院10 1 の 5 規則性 公倍数 気まぐれ解説カフェ 仮
正二十角形 二十角形 (にじゅうかくけい、にじっかっけい、Icosagon)は、 多角形 の一つで、本の 辺 と個の 頂点 を持つ 図形 である。 内角 の 和 は3240°、 対角線 の本数は170本である。③ 正n角形の対角線を全部掛けるとは? 正n角形について上図のように頂点を定めます。すなわち天辺をpとして左回りにp1、p2、、pn1と頂点に名前を付けます。この時、pp1の長さ(l1)は下図のように定義できます: p1はpのすぐお隣の頂点なので、オレンジ色の角度は360度(2π)を正n角形の「n」で割った値になります。



正多角形の辺と対角線
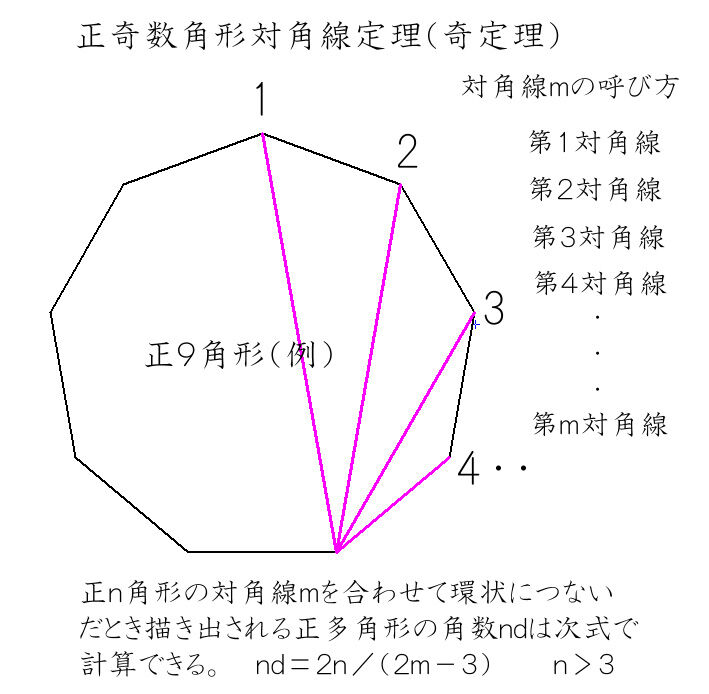



正多角形作図自由自在 正多角形第2定理 正多角形対角線定理 発想力教育研究所 素数誕生のメカニズム



お久しぶりです 中学受験算数角度正多角形で対角線をひくと 角度は Yahoo 知恵袋




正多角形の中心線と垂直に交わる対角線による分割された線分の2乗の和 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog




七角形 Wikiwand




正多角形の対角線




Inkscape 正多角形対角線を引いてみた パソコン備忘録




簡単公式 多角形の対角線の本数が5秒でわかる求め方 Qikeru 学びを楽しくわかりやすく




三角形の個数 Youtube




正多角形の重ね書きの青春 完全無欠で荒唐無稽な夢



1



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典
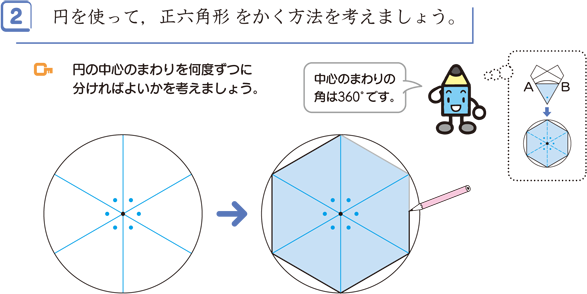



正多角形 算数用語集



図形 正十二角形の分解 父ちゃんが教えたるっ
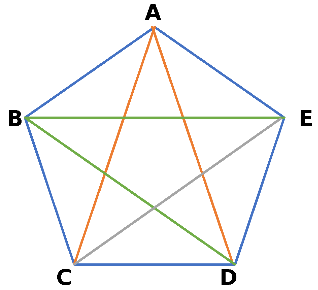



対角線 何本かな Gnolink 個別指導 グノリンク 知の力を活かせる人に




対角線とは 多角形の対角線の本数の2通りの求め方 算数パラダイス




多角形の対角線の作図は正確に書けると子供達は必ずはまります この喜びが子供を育ててくれます 七田式天六教室 本町教室及び魔法の折り紙オンライン教室は算数 数学のスペシャリストを育てます



1




高校数学a 正多角形内の三角形の個数 二等辺三角形 正三角形 直角三角形 鈍角三角形 鋭角三角形他 受験の月
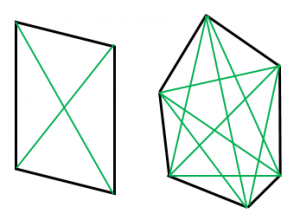



多角形の対角線の本数を求める公式 具体例で学ぶ数学
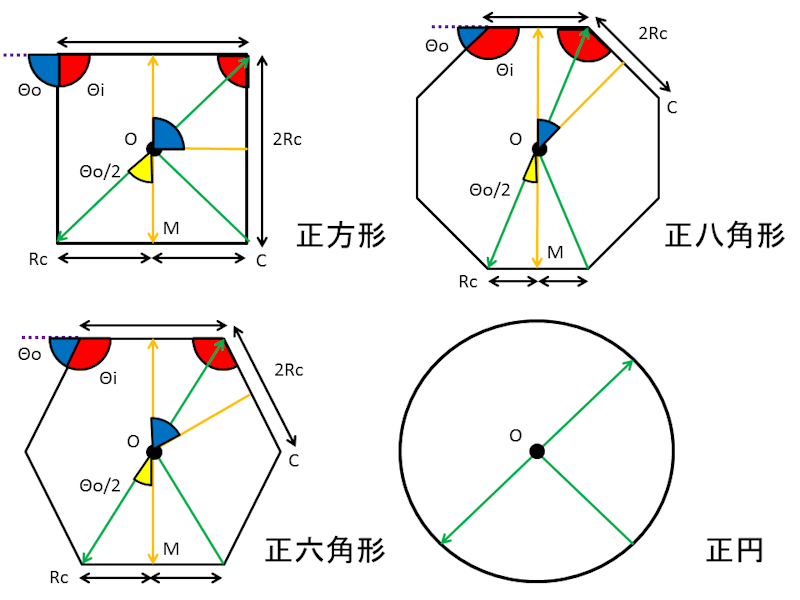



正多角形 Color Cube ウィキ Atwiki アットウィキ




正多角形の対角線の長さの種類 香料ゐっすゐの夢




Uzivatel 大前誰今夏一 衒学ゴールデン Na Twitteru Dodecagon正十二角形と正方形の裁ち合わせ誰だっけpickover様だっけ 似たような話 でネタにしたいけど見当たらないspecial Thanks ある正多角形の対角線を一辺とする面積が同じ別の正多角形になる例が欲しいぞ
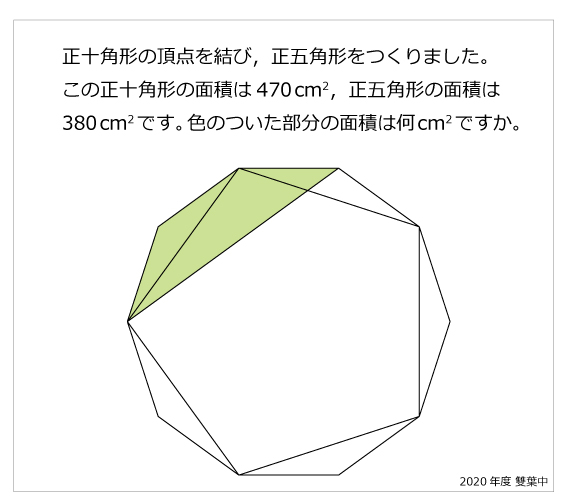



今年の1問 年雙葉中 正五角形と正十角形 算数星人のweb問題集 中学受験算数の問題に挑戦
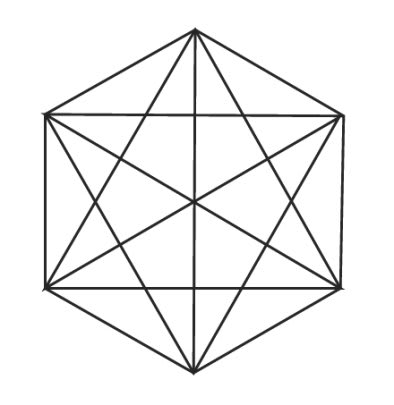



対角線の数って どうやって計算するんだ 名寄 算数数学教室より



正12角形と対角線 麻布中学 2010年 イメージでわかる中学受験算数問題




正八角形の対角線の本数 おときち副塾長 電脳空間学習塾かもん Youtube
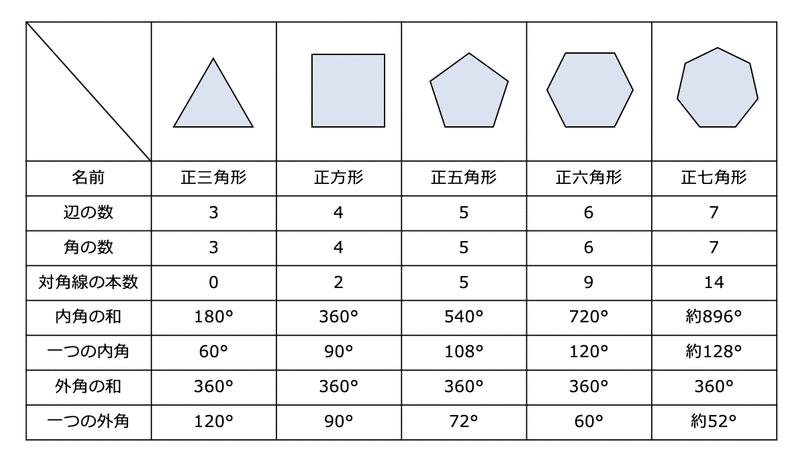



実践例 プログラミングで正多角形を学ぶ 山崎智仁 Tomohito Yamazaki Note




正多角形の対角線の長さ 香料ゐっすゐの夢



図形 正十二角形の分解 父ちゃんが教えたるっ
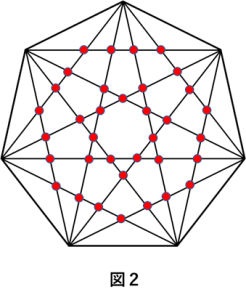



正九角形の対角線の交点の数を求める 中学受験プロ講師ブログ




十角形の対角線 アセント学習塾 塾長の こうかい 日誌




単位円に内接する正n角形の1つの頂点から他の頂点にひいた線分の積 数学の偏差値を上げて合格を目指す
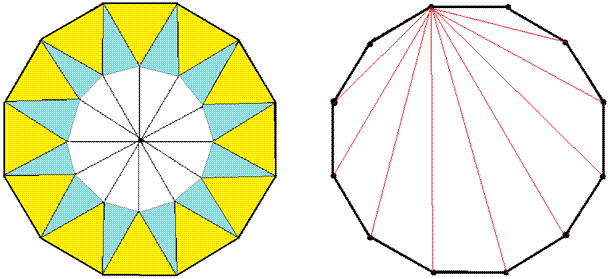



問題187 正十二角形の秘密



図形 正十二角形の分解 父ちゃんが教えたるっ
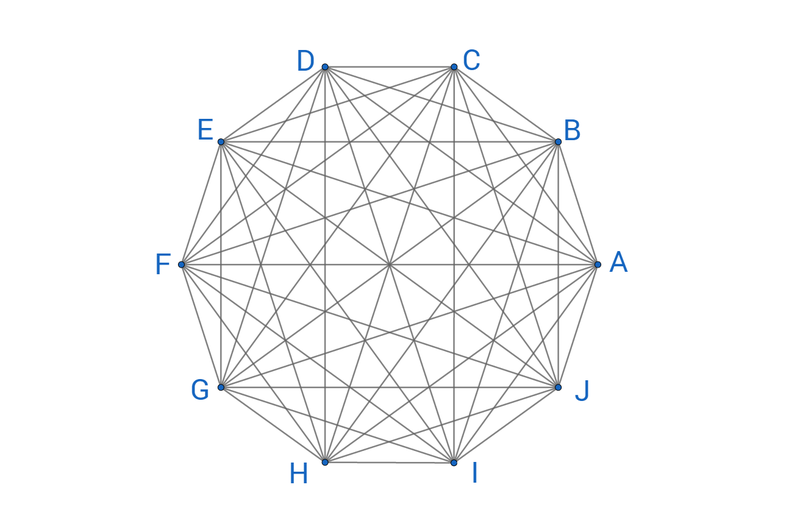



十角形の対角線 アセント学習塾 塾長の こうかい 日誌




素数誕生のメカニズム Art32pazuru なぜそんな形になってしまうんですか 正五角形にはペンタゴンーデカゴン定理や正多角形の角数nについて倍角数定理が存在しています 正多角形作図自由自在 正多角形第2定理 正多角形対角線定理 発想力教育研究所 素数誕生の
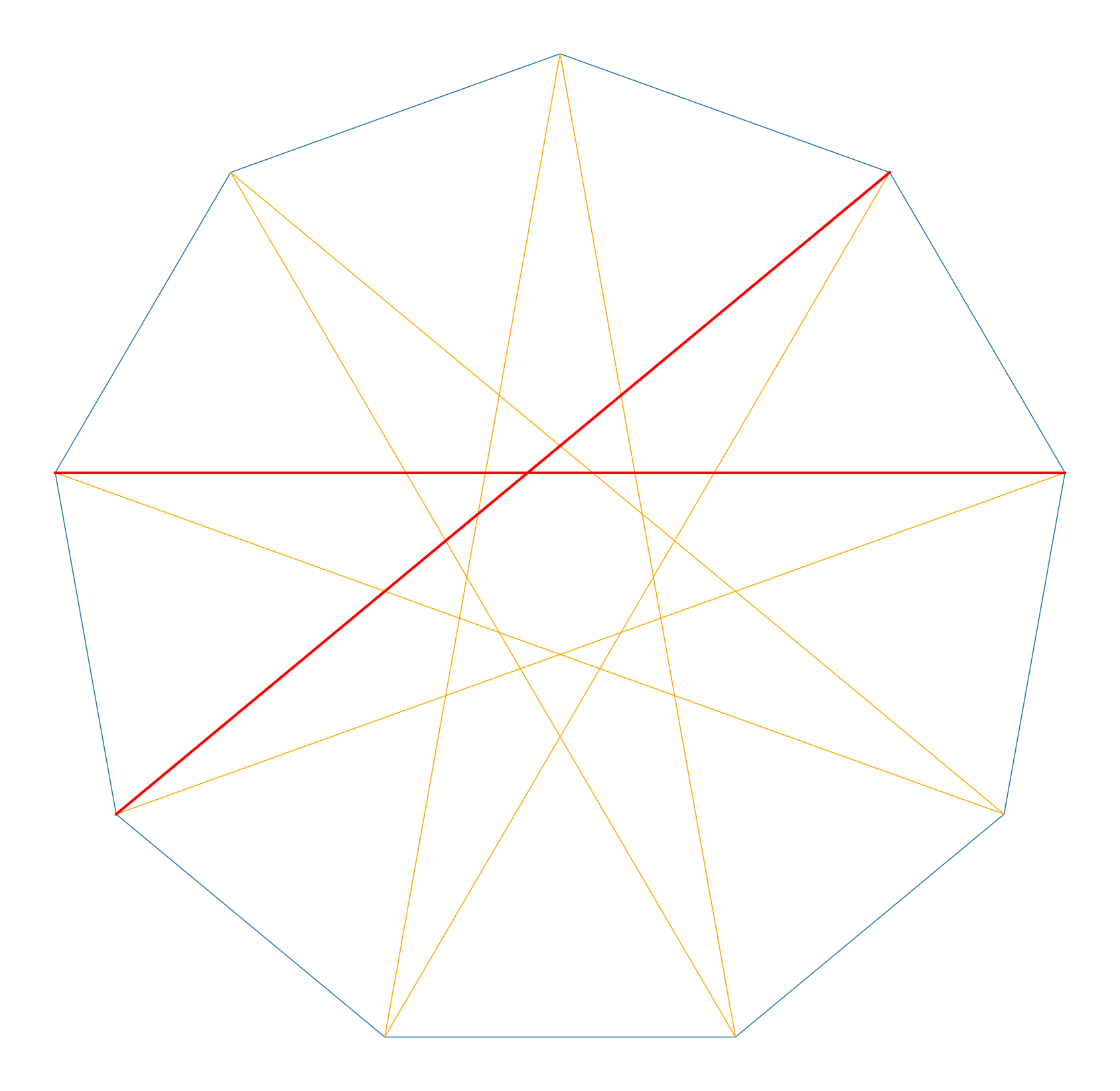



正多角形とその対角線によって作られる正多角形の相似比 Yhoka Com



三角関係になった事がある人いますか ガールズちゃんねる Girls Channel
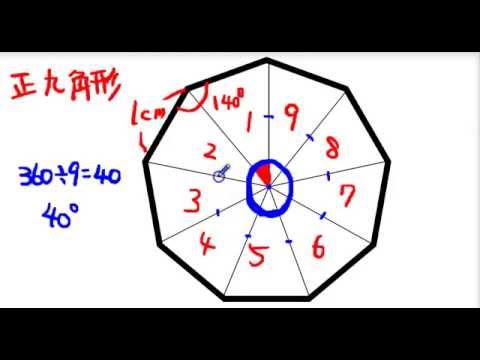



正多角形の性質 正九角形を例に Youtube
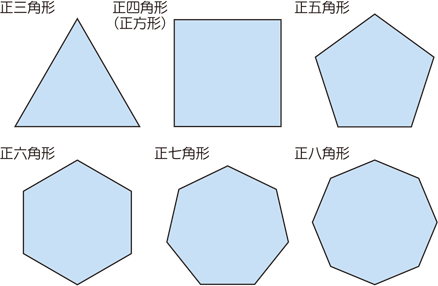



正多角形 算数用語集




二十角形 Wikiwand




正多角形 Wikipedia
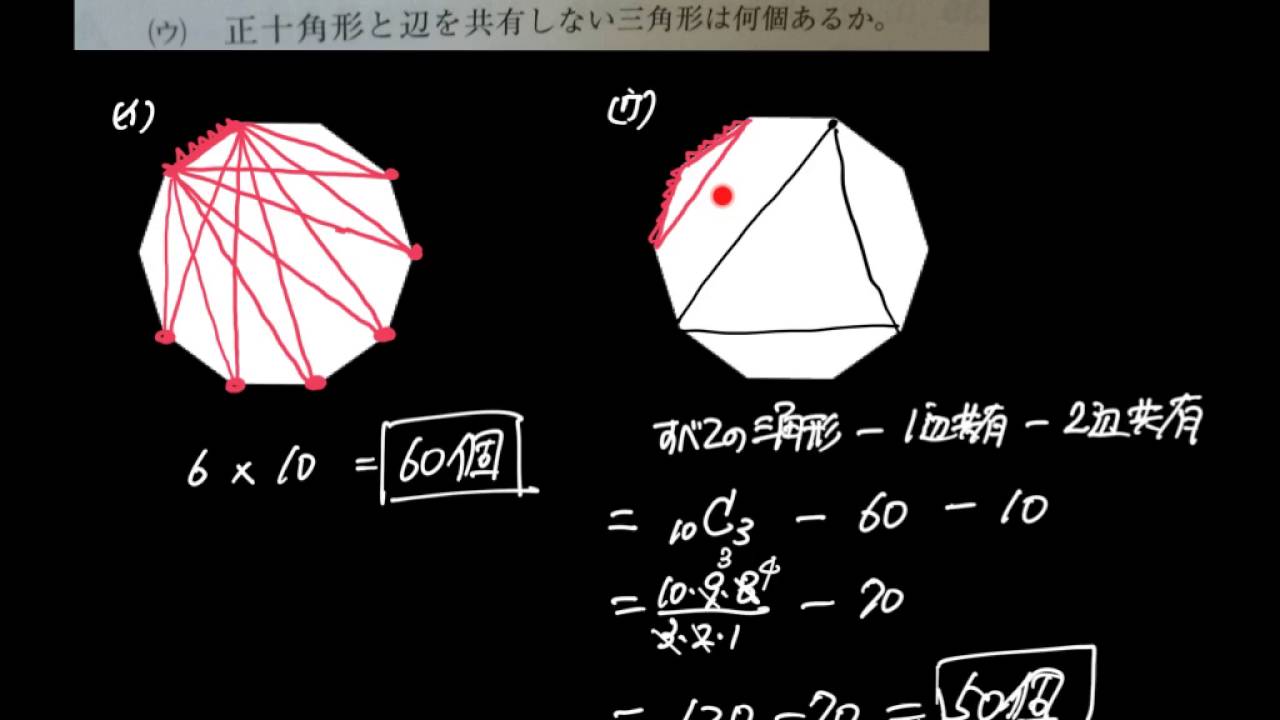



数a 正10角形 一辺を共有する三角形 Youtube




ハは肺魚のハ 跡地 直径10cmの正十二角柱型プリンの体積の求め方



正十角形の問題の解説をお願いします 正十角形において 1 対角線は Yahoo 知恵袋




頂点間の長さの種類の個数を求める問題 17年 広尾学園中学校 恋する中学受験 大学受験を見据えた中学受験




正二十四角形の対角線を幼稚園年長児に作図してもらっています みんな感動します 七田式天六教室 本町教室及び魔法の折り紙オンライン教室は算数 数学のスペシャリストを育てます



正十角形出るとオモタよ ジュニア算数オリンピック18 父ちゃんが教えたるっ




正多角形の対角線 あなたと夜と数学と



図形 正十二角形の分解 父ちゃんが教えたるっ



1
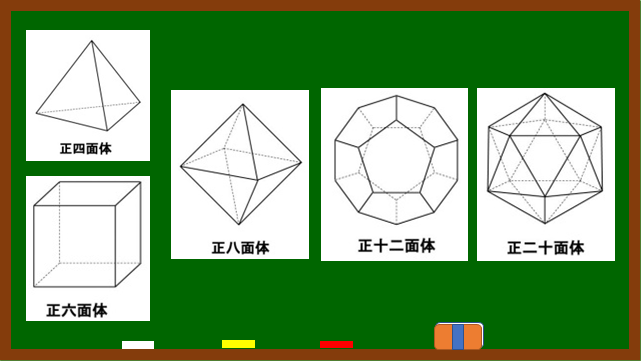



たのしい算数 正多角形はキレイだからこそ キッズライト 公式サイト 福岡 西都小学校前の学童保育 学習塾 四谷大塚net 東進こども英語塾



小学校6年生 算数 正多角形の対称 Youtube




十三角形 Wikipedia
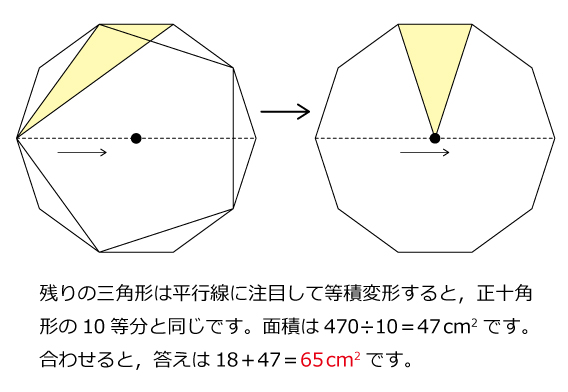



今年の1問 年雙葉中 正五角形と正十角形 算数星人のweb問題集 中学受験算数の問題に挑戦
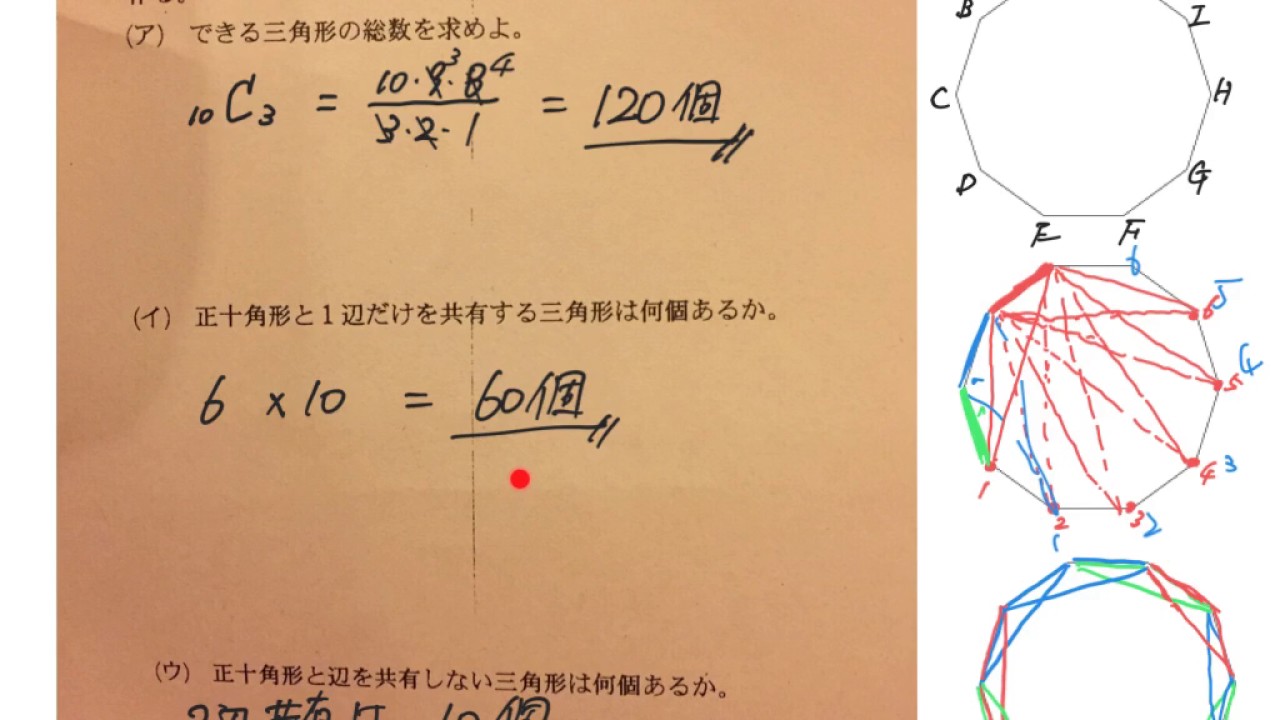



数a 正10角形 辺を共有しない三角形 Yokohama Youtube



いろいろな正多角形をかいてみよう 家庭学習レシピ



正17角形と正18角形



十二角形 Wikipedia
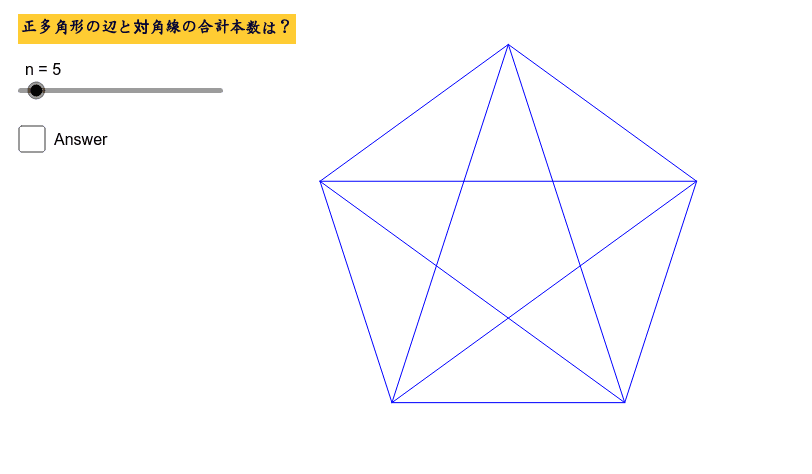



正多角形の辺 対角線の本数 Geogebra




Scratch Search



図形 正十二角形の分解 父ちゃんが教えたるっ




十角形 Wikipedia
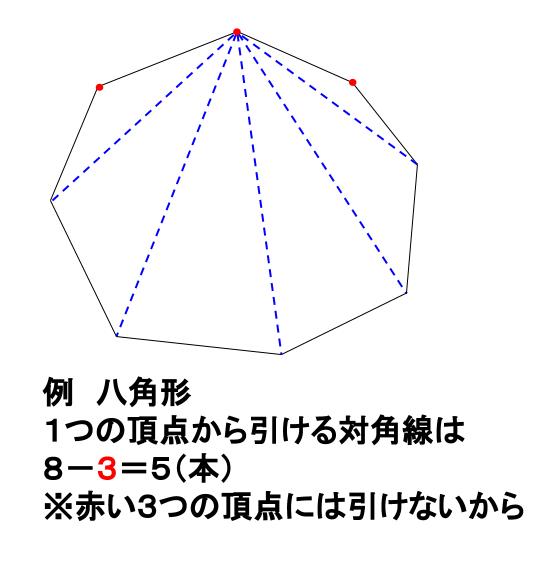



中学数学 多角形の対角線の本数 中学数学の無料オンライン学習サイトchu Su




二百五十七角形 Wikipedia



Cmsweb2 Torikyo Ed Jp T Chu Kyou Shin Action Common Download Main Upload Id 116




小5 算数 小5 54 正多角形 Youtube
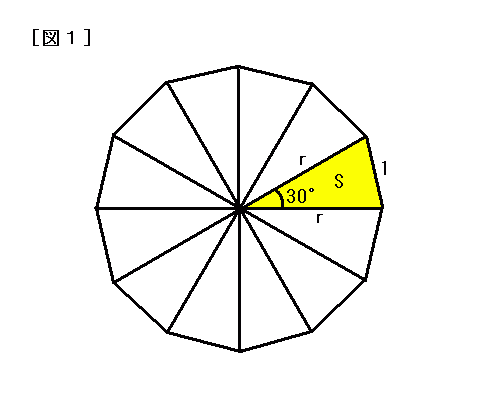



問題187 正十二角形の秘密




正10角形と等積変形 21年jmo 予選 第二問 数学日和




正多角形の対角線 あなたと夜と数学と



対角線を描く すぐる学習会
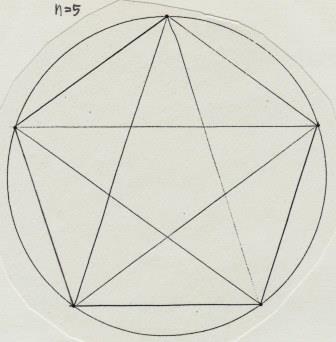



正多角形の対角線 あなたと夜と数学と



第390問の解答




簡単公式 多角形の対角線の本数が5秒でわかる求め方 Qikeru 学びを楽しくわかりやすく



図形 正十二角形の分解 父ちゃんが教えたるっ




簡単公式 多角形の対角線の本数が5秒でわかる求め方 Qikeru 学びを楽しくわかりやすく




正四十八角形対角線を書くお母様が出現しました 七田式天六教室 本町教室及び魔法の折り紙オンライン教室は算数 数学のスペシャリストを育てます




正多角形 せいたかっけい とは ピクシブ百科事典
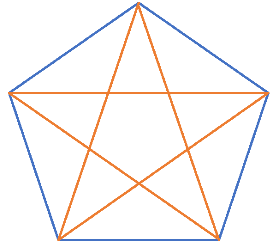



対角線 何本かな Gnolink 個別指導 グノリンク 知の力を活かせる人に




正多角形の対角線 あなたと夜と数学と




簡単公式 多角形の対角線の本数が5秒でわかる求め方 Qikeru 学びを楽しくわかりやすく
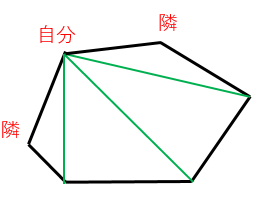



多角形の対角線の本数を求める公式 具体例で学ぶ数学




対角線とは 多角形の対角線の本数の2通りの求め方 算数パラダイス



対角線 何本かな Gnolink 個別指導 グノリンク 知の力を活かせる人に




正多角形の対角線
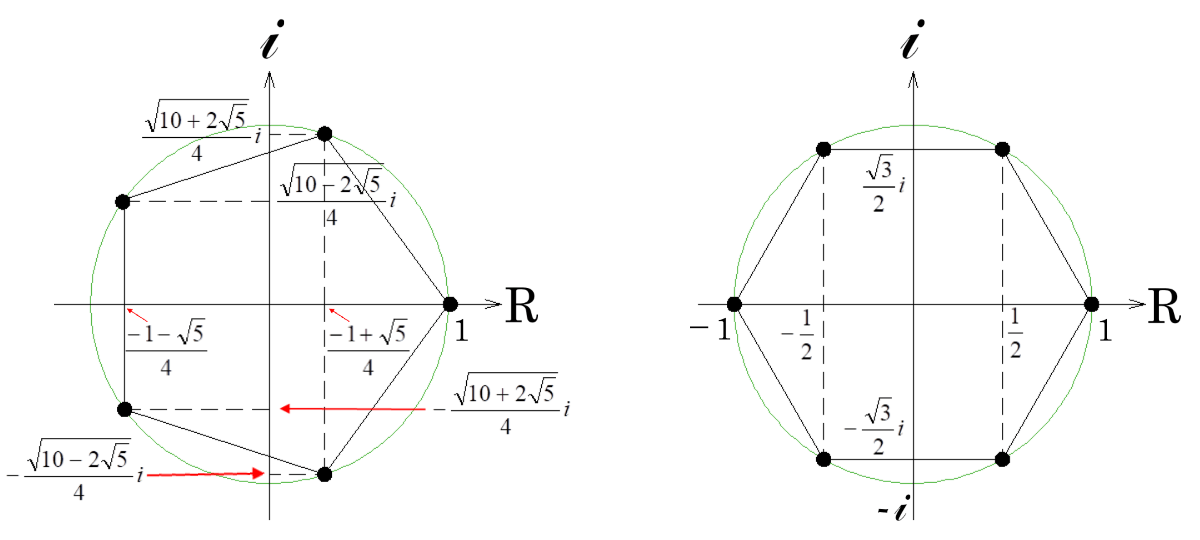



正多角形と方程式 X N 1 0 の不思議な関係 勉強法のバイブル 帝都大学へのビジョン



正多角形の対角線




簡単公式 多角形の対角線の本数が5秒でわかる求め方 Qikeru 学びを楽しくわかりやすく




おぉ 寒い寒い 正多角形の対角線



0 件のコメント:
コメントを投稿