平行線と線分の比 1 課 題 平行線の性質をもとにして、生徒たちが調べたこ とをそれぞれ生徒に説明(証明)させるという課題 学習である。生徒一人一人が自分で課題を設定し、 自分の力で証明していくのであるから、学習内容は 生徒によって異なる。平行線と線 分の比 平行線と線 分の比に関 する性質を 見いだし,そ れを証明し, 利用するこ とができる。 三角形の1つの 辺に平行な直線 を引き、そこに できる線分の比 について長さを 調べ、それを証 明する。 平行線と線分の 比についての性質 に関心平行線と線分の比 まとめ 以上、7パターンの問題について解説してきました。 おそらくこれらのパターンをしっかりと理解できていれば ほとんどの問題には対応できるのではないかと思います。 比の取り方は、練習で身につけていくのが一番です。
1
平行線と線分の比 証明
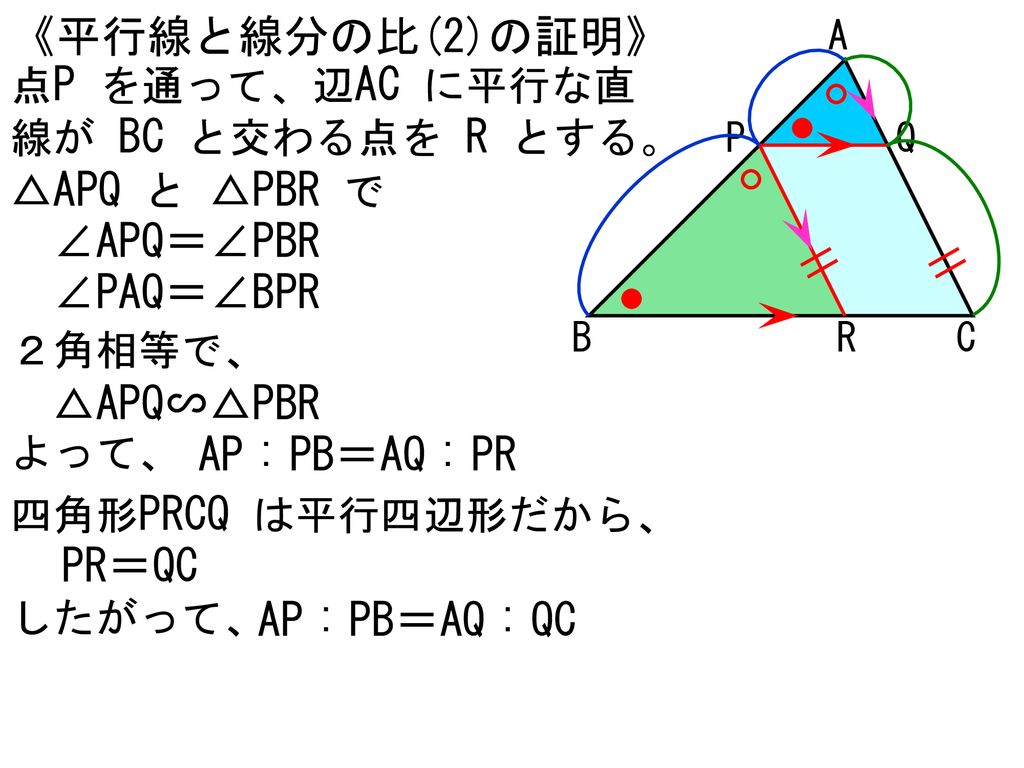
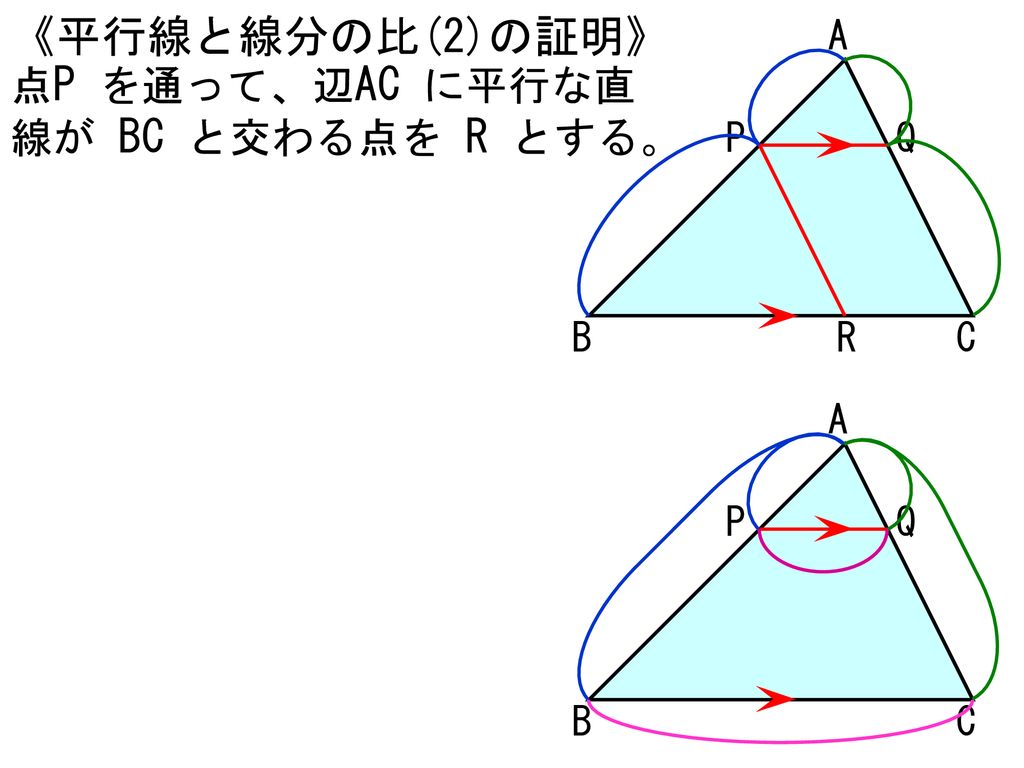
平行線と線分の比 証明-《平行線と線分の比(2)の証明》 a b c p q 点p を通って、辺ac に平行な直線が bc と交わる点を r とする。 r apq と pbr で ∠apq=∠pbr ∠paq=∠bpr 2角相等で、 apq∽ pbr よって、 ap pb=aq pr 四角形2/5時 ・ 平行線と線分の比に関する性質を理解する。 ・ 平行線と線分の比の性質を利用して、辺の長さを求めることができる。 前時のまとめを基に、平行線と線分の比の性質について確認する。 本時の学習内容「平行線と線分の比の関係について
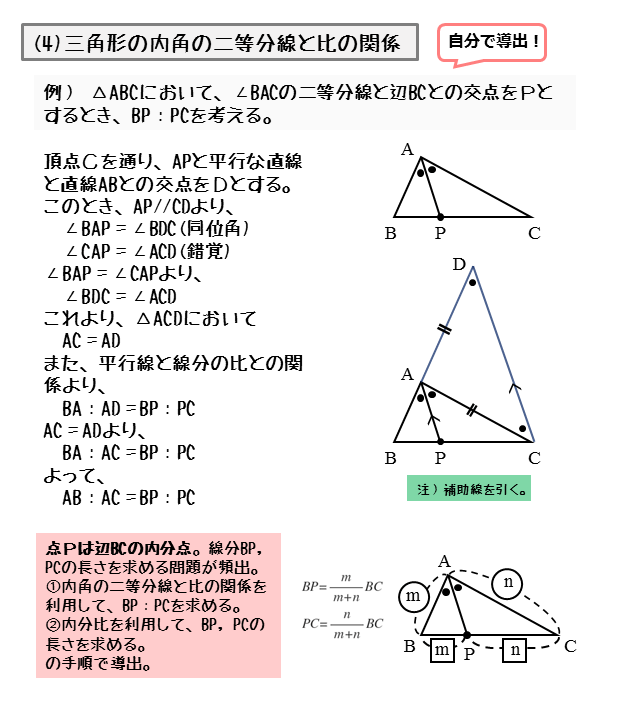



図形の性質 角の二等分線と比について 日々是鍛錬 ひびこれたんれん
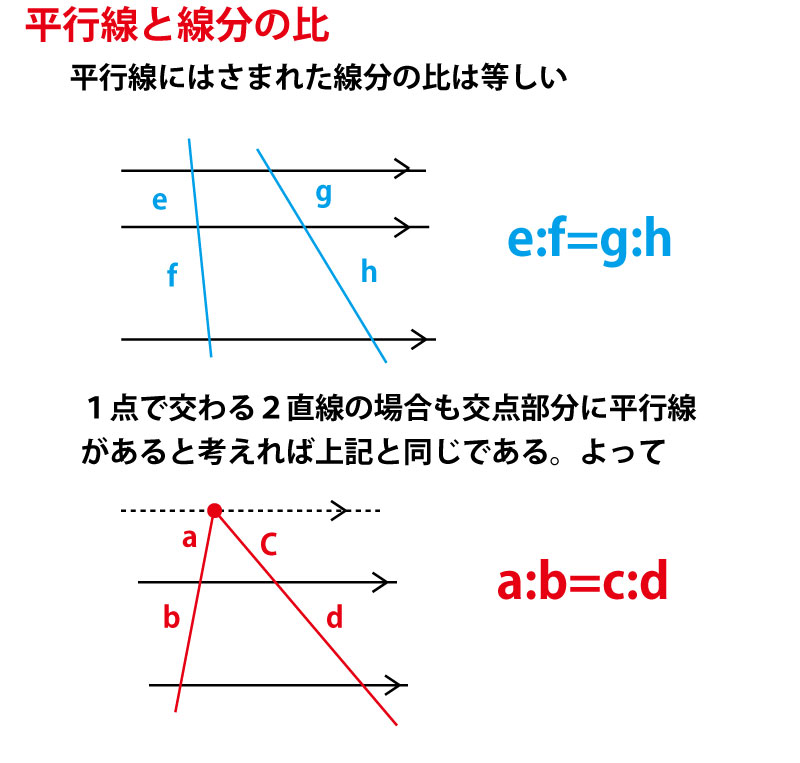
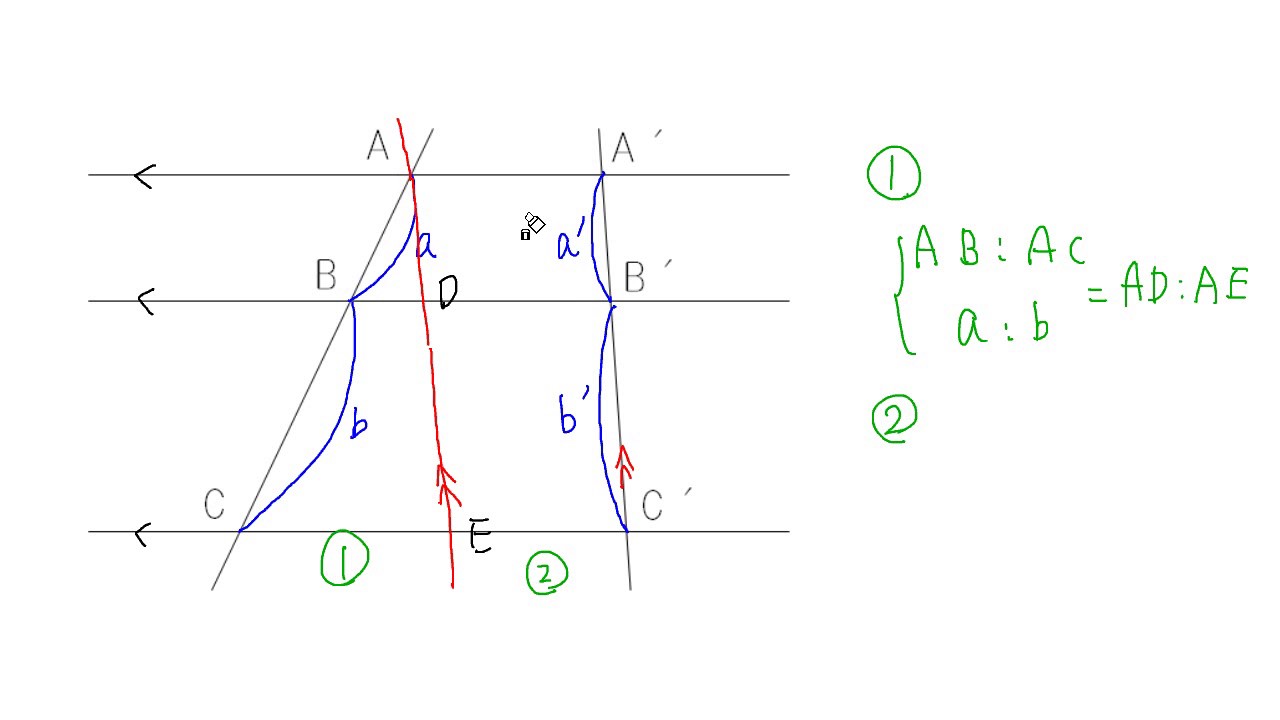
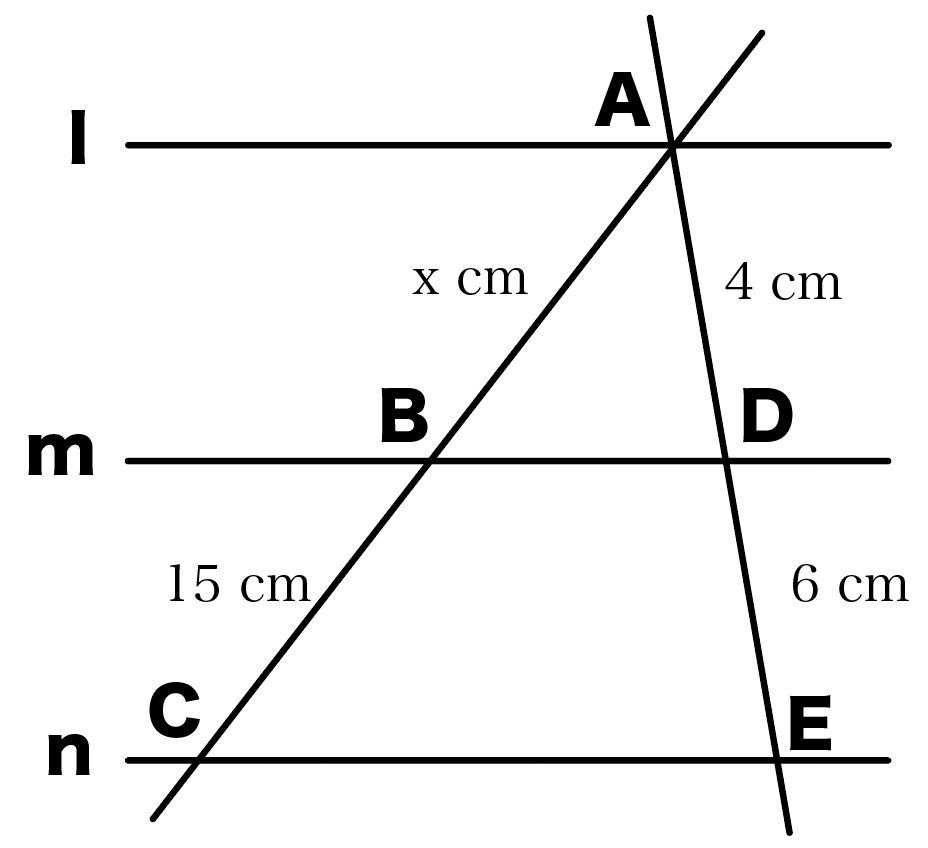
三角形と線分の比/平行線にはさまれた線分の比/平行線と線分比応用/ 三角形の角の二等分線と線分の比 /中点連結定理:証明問題/長さ・角度の計算/全般/ FdData 中間期末製品版のご案内 FdData 中間期末ホームページ平行線と線分の比 下の図で、直線 \(l,m,n\) が平行ならば、線分の長さの比について以下のことが成りたつ。 \(abbc = deef\) これはなぜ成り立つのか。 下の図のように、\(df\) と平行な線分・ 平行線と線分の比の性質を使って証明を考えることができる。 ・ 平行線と線分の比の性質を利用して、辺の長さを求めることができる。 段階
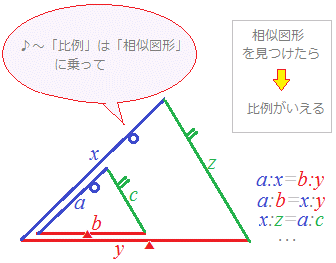
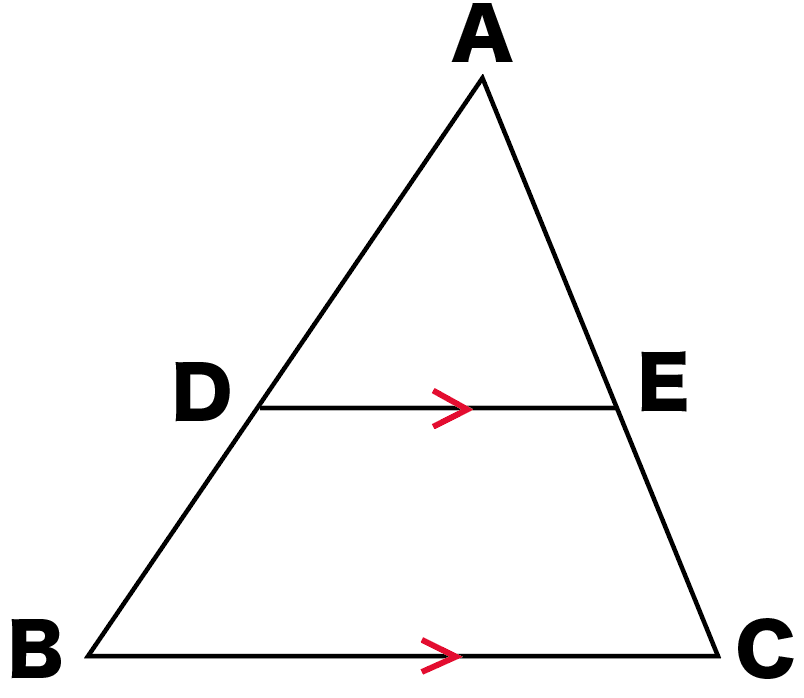
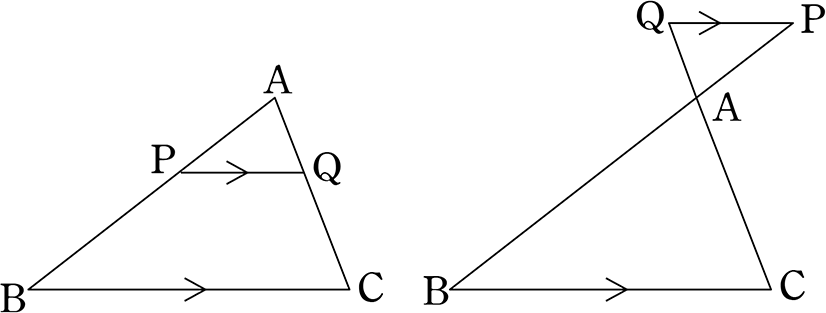
平行線と線分の比 $ap:ab=aq:ac=pq:bc$ となる。 注:これは覚える必要はありません。 簡単に証明できるからです。 平行線の線分比の性質を使った問題です。 図形を見てどことどこが相似になりそうかわかるようになると良いですね。 相似であることを証明する問題です。 証明問題は嫌われがちですが、本質的に今までの角度や長さを求める問題とあまり変わりません 三角形と平行線の線分の比 まずは 三角形と平行線の線分の比の ルールを覚えましょう。 ポイントは ①2つの辺が平行であれば ②どの辺の比の関係が成り立つのか を押さえる というところになります。
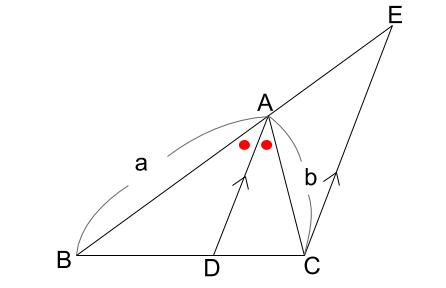
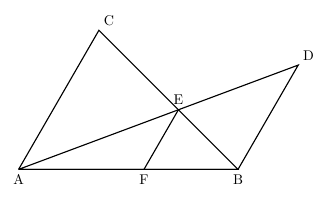
今回は中2で学習する『平行線と線分』という単元から 等積変形という問題を解説していきます。 等積変形というのは 面積の等しい三角形を見つける問題や 面積が等しくなるように図形を変形する問題です。 まずは、等積変形をやっていく上で なぜ、この補助線を書いたかというと、 この補助線があると、平行と線分比の関係をうまく使えるからなんじゃ 具体的に見ていくかのぉ まず、ax xd を考えてみるかのぉ 図で考えると、ax xd というのは、以下の感じじゃ 最後に、平行線と線分の比から $$\begin{eqnarray}ABAE(AC)=BDDC \end{eqnarray}$$ となります。 まとめ! お疲れ様でした! 内角の二等分線と比の性質は入試でもよく出題されます。 なので、絶対に覚えておきたいですね。




中学校数学 証明のコツ 年03月



平行線と線分の比の定理の逆は成り立たない反例を教えて下さい 図を描 Yahoo 知恵袋
似 10 「平行線と比」の定理を利用して,線分 課題把握,解決の見通しや確認を行う。 の長さなどを求めることができるようにす る。 の 応 11 三角形の2辺を等しい比に分ける2点を結 べば,その線分は残りの辺に平行となること 用 を考えさせる。平行線 と線分 の比の性質 を使 って 、いろい ろな 線分 の長さを 求 めることができ る。 いくつかの 平行 線が他の直線 と交 わってできる 線分 の比の性質 を理解 する 。 2 平 行 線 と 比 第 6 時 平行線 と線分 の比の性質 を利 用して 、図形 のい ろいろ平行線と線分の比の性質を証明するには,三角形と比の定理を用いればよいことに気付 き,証明をすると共に,その性質を用いて線分の長さを求めることができる。 ②コンピュータ活用の意図 ・「直線を移動させる機能」を使って,「三角形と比の定理




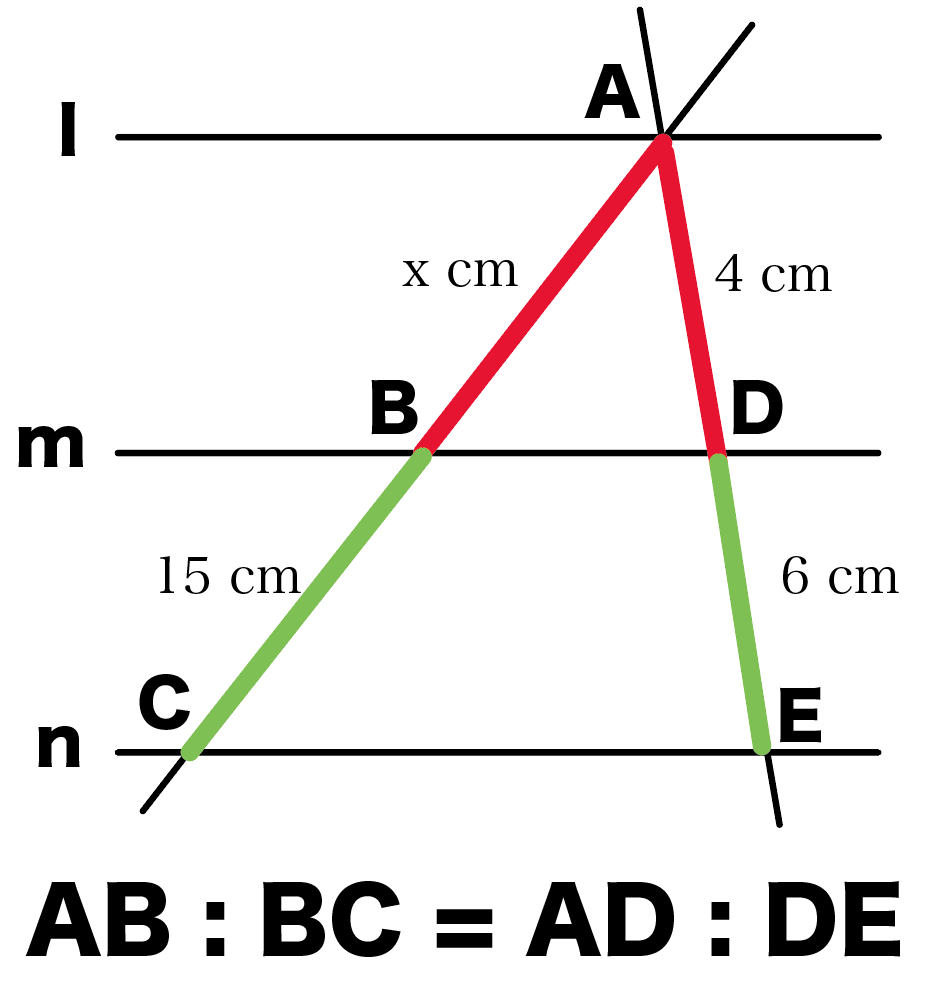
平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1
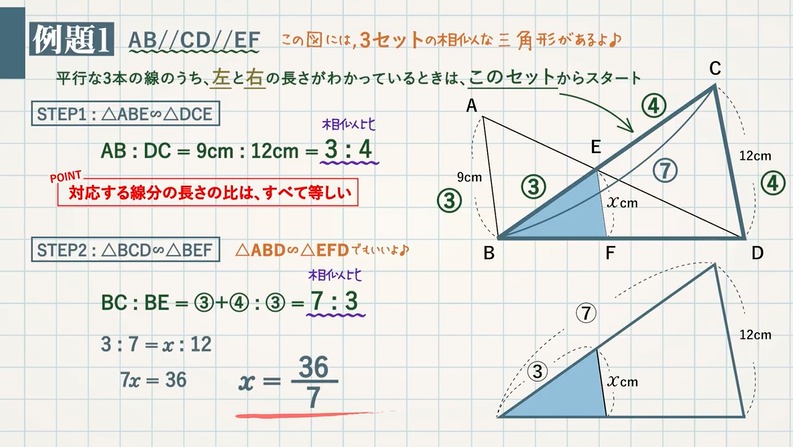
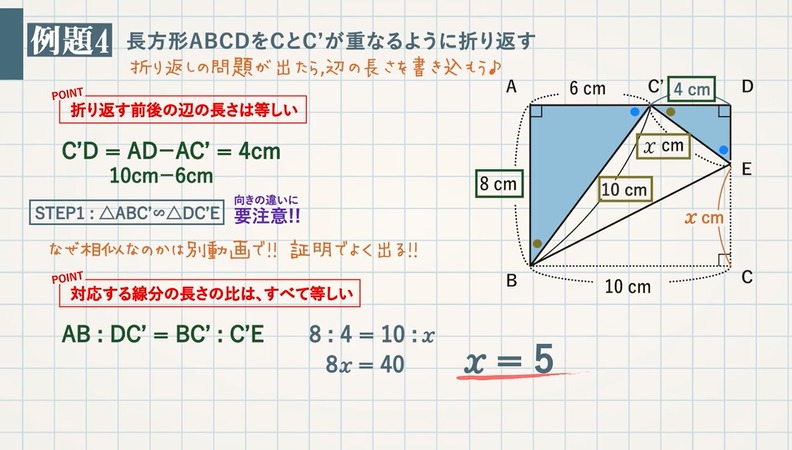
4 平行線と線分の比 平行な直線がある2つの三角形の線分の比について1 abc でpq¥bc のとき、 apq は abc と相似になる。 <証明> apq と abc において pq¥bc より、 平行線の同位角は等しいから ∠apq =∠abc ① ∠aqp =∠acb ② (∠a が共通も使えるけどね)相似比を活用することで、\(AE=15\) と求め、 \(y=15=5\) と求めることもできますし、 下図の赤と青の線分の比が \(186=31\) であることを用いて \(y=×\displaystyle \frac{1}{31}=5\) と求めることも可能です。 次のページ 平行線と線分の比 ;平行線と線分の比の利用 平行線と線分の比を用いる問題を練習しましょう。 \(2\) つの似ている図の問題を比較して、平行線と線分の比の利用について理解を深めましょう。 例題1 次の図で、直線 \(l,m,n\) が平行




平行線にはさまれた線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく




平行線と線分の比 の勉強法のわからないを5分で解決 映像授業のtry It トライイット
対頂角、平行線の性質と条件 相似な図形、相 図形の性質の調べ方 三角形の合同条件 平行線と線分の比 証明のしくみ 中点連結定理 5章 平面図形(中1学年) 対称な図形 垂線の作図 線分の垂直二等分線 角の二等分線平行線と台形中3数学 問題をノーヒントでやってみよう 略解をチェックしよう 攻略ポイントを確認しよう ・平行線で三角形を作り、線分の比を利用する 完璧じゃなかったら授業動画を見よう やる気先生の授業動画 326K subscribers=== 平行線と線分の比 === 三角形の相似条件 次の(1)(2)(3)は三角形の相似条件と呼ばれており,そのうち1つでも成り立てば2つの三角形は相似になる. 逆に,2つの三角形が相似であるとき,次の(1)(2)(3)はすべて成り立つ.




中学3年数学練習問題 図形と相似 平行線と線分の比の問題



16年前期 千葉県公立高校入試 数学 第2問 5 作図 解答 解説 船橋市議会議員 朝倉幹晴公式サイト
平行線と線分の比 右の図で,AB == PQ == CD である。 a b x A B C D P Q AB = a;動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru 平行線と線分の比で下の写真の三角形の比が 22+3=25 とあったのですがこの式はいったいどういう理屈で出てきたかわかりません 何故22という 比が出てきて更に3を足すのですか、何



平行線と線分の比 辺の長さを求める応用問題4選 教遊者



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
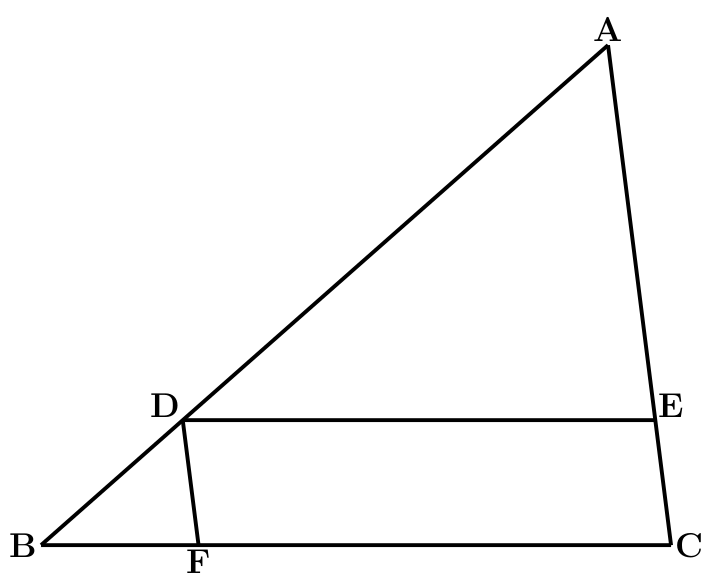
(平行線と線分比) 3角形の角の2等分線の定理 問1 ABCの内角 Aの2等分線が辺BCと交わる点をDとする。 内角 Aの外角の2等分線が辺BCの延長線と交わる点をEとする。 AB:AC=BD:CD平行とは 同一の平面上にあって、 両方向に限りなく延長しても、 いずれの方向においても互いに交わらない直線 ・ (数学的証明) Oから直線lとその平行線mに 垂線 を下す (三角形の内角の和は180°) {∠a =180°−90°−∠O( OaAにおいて) ∠b =180°−90°−∠O( ObB線分 ec と対角線 bd との交点を f とし,点 f を通って辺 bc に平行な直線と辺 ab との交点を g とします。 このとき,線分 EG の長さを求めなさい。 (埼玉県17年入試問題)



中3数学 平行線と線分比の利用のポイントと練習問題




平行線と線分の比 の問題のわからないを5分で解決 映像授業のtry It トライイット
単元 合同な図形と証明,三角形, 「_三角形と線分の比 _平行線と線分の比 pointまとめ. 復習&おさらいにどうぞ🌷」, 学年 中学2年生, キーワード 数学,相似,平行,比,三角形,平行線,中2,図形,幾何,定理,まとめ,math平行線と線分の比の 性質を理解すること ができる。 5 単元計画(8時間) 次 時 学習活動・内容 生徒の思考 指導・援助の手だて 1 (1) 1 平行線と線分の比についての課題を見いだす。 (1) 実測できない線分の比について考える。 平行線 行線 れそうだぞ数学35章図形と相似「平行線と線分の比」<基本問題①・解答> 1 説明※平行線は,三角定規を利用してかく。 ①図のように線分AC上で点Aから 7番目の点と点Bを結ぶ。 ②点Aから5番目の点を通り,①で ひいた線分と平行な線分をひく。



至急 平行線と線分の比の逆の証明を教えてください Ad Db Yahoo 知恵袋



平行線と線分の比
平行線と線分の比 右図2のような図形において幾つかの辺の長さが分かっているとき,未知の辺の長さを求めるために図1の黄色の矢印に沿って辺の長さを求めることができる. bd//ce のとき まず (2) ∽ であることを証明しなさい。 線分の長さの情報がありません。 こういう時は大体「2組の角がそれぞれ等しい」を使います。 ※線分の長さや比がわからなくても「中点」「重心」「角の等分線」等の情報を使って比を求める事ができる場合もあります。PQ = x とするとき, x = ab a b が成り立つ. £ ¢



平行線と線分の比 Youtube



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学
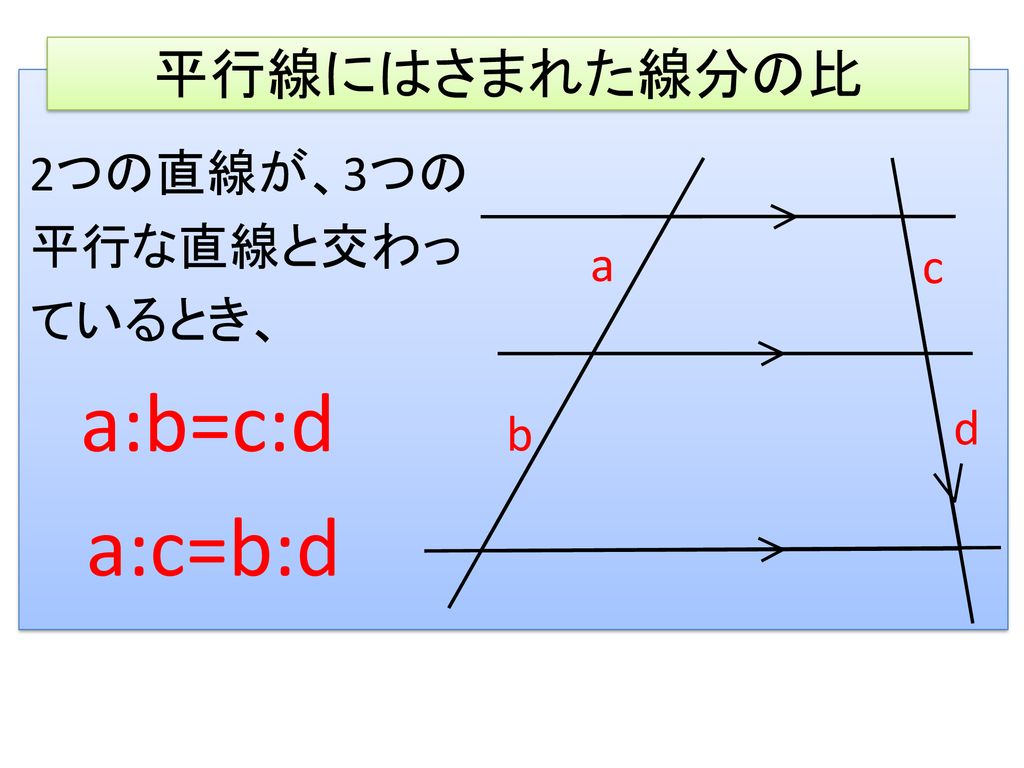
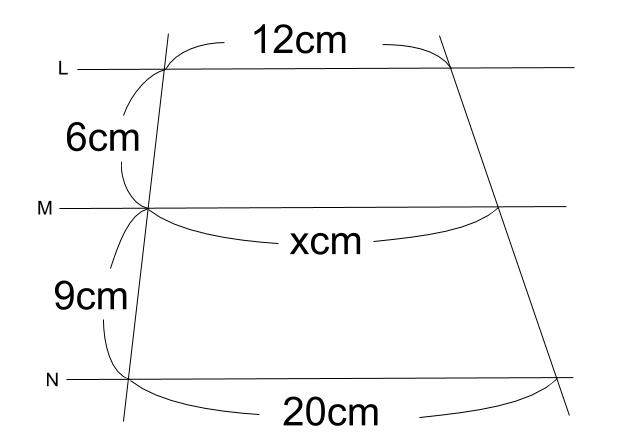
平行線で区切られた線分の比の定理 「平行線と比の定理」の 型と 型は、台形のようなものにも応用できますね! 直線 t を平行移動させた t' も、 当然 a':b' ですね! (t と t' の間の空間は平行四辺形) 実は、3本の平行線(に交わる直線の「 比 」は「平行線と線分の比の定理」の問題の解き方 管理人 5月 5, 三角形の相似条件と証明問題の解き方 図形を拡大・縮小したものを相似といいますが、三角形の場合、相似であることを証明するための条件があります。√2が無理数である証明, 実数 = {有理数, 無理数} 点と直線の距離の公式 証明;



平行線と線分の比 中学3年 数学クラブ




世界一わかりやすい数学問題集中3 5章 図形と相似
Intercept theorem は,2本の交わる直線と複数の平行な直線が交わってできるsegment(平行な直線によって切り取られる線分)の比が等しいという定理で,図1の場合なら a:b=c:d が成り立つという定理です.日本の中学数学3の教科書では,「平行線と線分の比



平行線と線分の比の証明 浅野直樹の学習日記




平行線と線分の比 中学校数学 2018年度高崎経済大学経済学部 地域政策学部入試問題 身勝手な主張




平行線と線分の比と中点連結定理 数学の要点まとめ 練習問題一覧




中2 相似 平行線と線分の比 中学生 数学のノート Clear




平行線と線分の比 三角形の比の取り方を簡単な問題で覚えよう 中学や高校の数学の計算問題
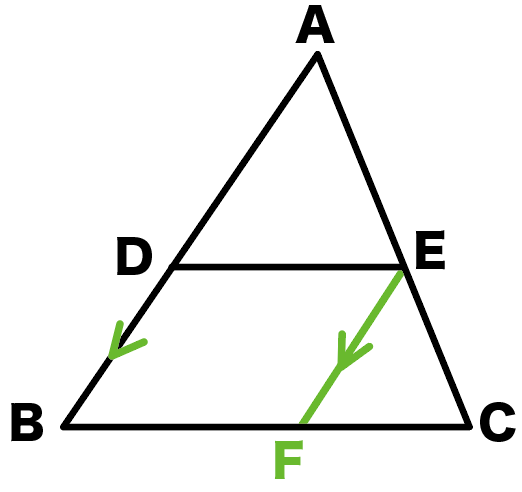



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく




中3数学 相似な図形 Abcに二等分線をひいたとき Ab Ac Dc の証明 Youtube



平行線と線分の比




線の引いてあるところで 平行線と線分の比はわかるのですが どう考えれば下線部のように Clear



角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su




平行線と線分の比 無料で使える中学学習プリント



本時のねらい 三角形の1辺に平行な直線が他の2辺と交わるとき それぞれの交点は その2辺を等しい比に分けることを理解する Ppt Download




数学 平行と線分比をシッカリわかると メネラウスの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生




世界一わかりやすい数学問題集中3 5章 図形と相似
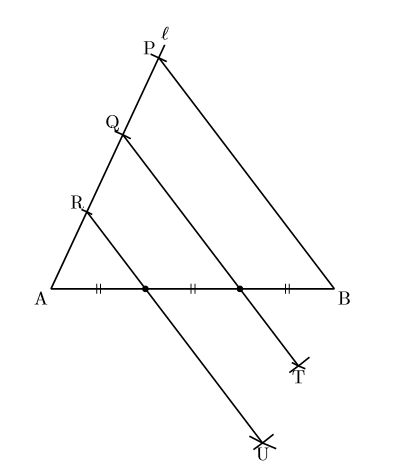



中学数学 3等分線を考える 数樂管理人のブログ




平行線と線分の比 の問題のわからないを5分で解決 映像授業のtry It トライイット




平行線と線分の比 の問題のわからないを5分で解決 映像授業のtry It トライイット



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく




図形の性質 角の二等分線と比について 日々是鍛錬 ひびこれたんれん



1



平行線と線分の比 辺の長さを求める応用問題4選 教遊者



5 図形と相似 1章 図形と相似 4 平行線と線分の比 5時間 Ppt Download



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su




中学校 数学 3年 5章 8 平行線と線分の比は簡単 これだけ覚えとこう ワカデキな中学校数学




中2 相似 平行線と線分の比 中学生 数学のノート Clear



5章2節01 平行な三角形と辺の比その1 中村 翔



高校入試 英語 数学 図形と相似 平行線と線分の比




平行線と線分の比 の問題を参考に 問題へのアプローチを 現役医師による難関高校受験塾 Core コア




中3数学 相似と線分比1 平行四辺形 Youtube



中学校3年生の数学の授業
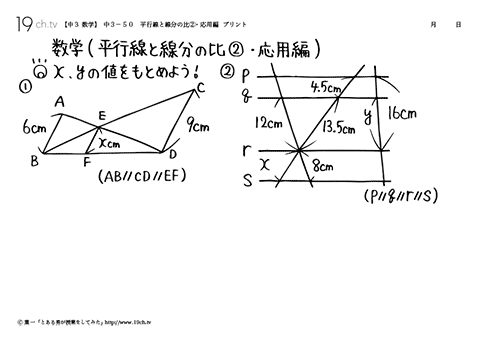



中学3年の数学 動画 平行線と線分の比 応用編の問題 19ch



Studydoctor三角形と平行線の比の証明 中3数学 Studydoctor




数学 中3 49 平行線と線分の比 基本編 Youtube



平行線の線分比の問題の解法 夢を叶える塾




平行線と線分の比の証明 浅野直樹の学習日記



Http Hokusuukyou Cyuu Com 14 3 Zukei Pdf



中学数学 図形の相似



1



5 図形と相似 1章 図形と相似 4 平行線と線分の比 5時間 Ppt Download
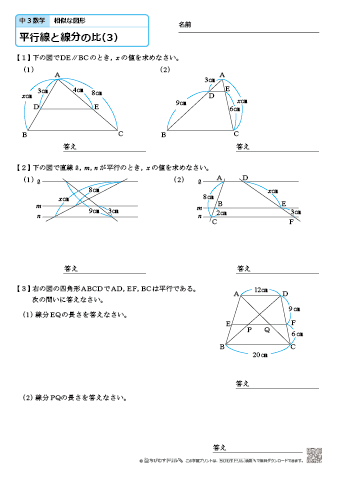



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




平行線と線分の比 Ict教材eboard イーボード




平行線と線分の比と中点連結定理 数学の要点まとめ 練習問題一覧
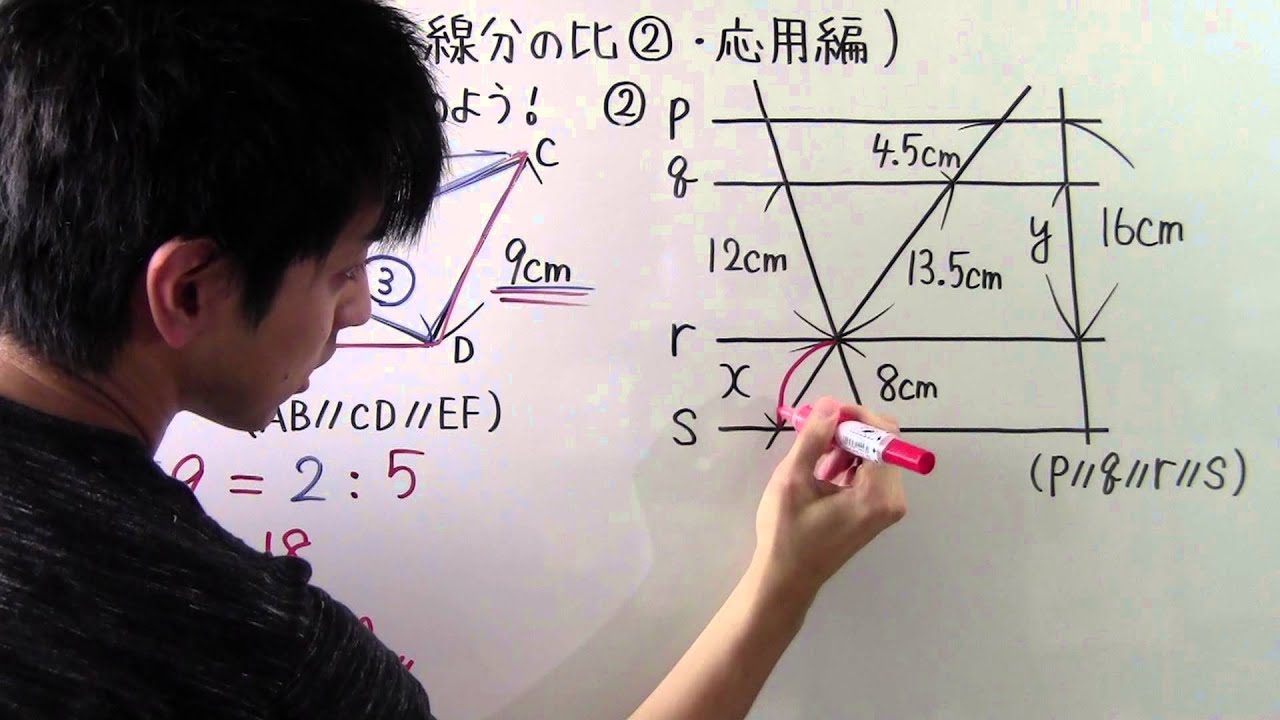



数学 中3 50 平行線と線分の比 応用編 Youtube




大泉英数研究室 数学 ブログ 11 16 数学




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学



Studydoctor平行線と線分の比の利用 中3数学 Studydoctor




中学数学3 平行線と線分の比の証明 中学数学 By となりがトトロ マナペディア



平行線と線分の比 辺の長さを求める応用問題4選 教遊者
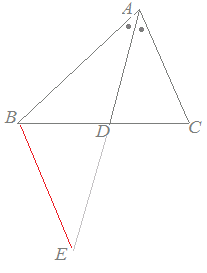



角の二等分線と補助線



平行線と線分の比 中学3年 数学クラブ
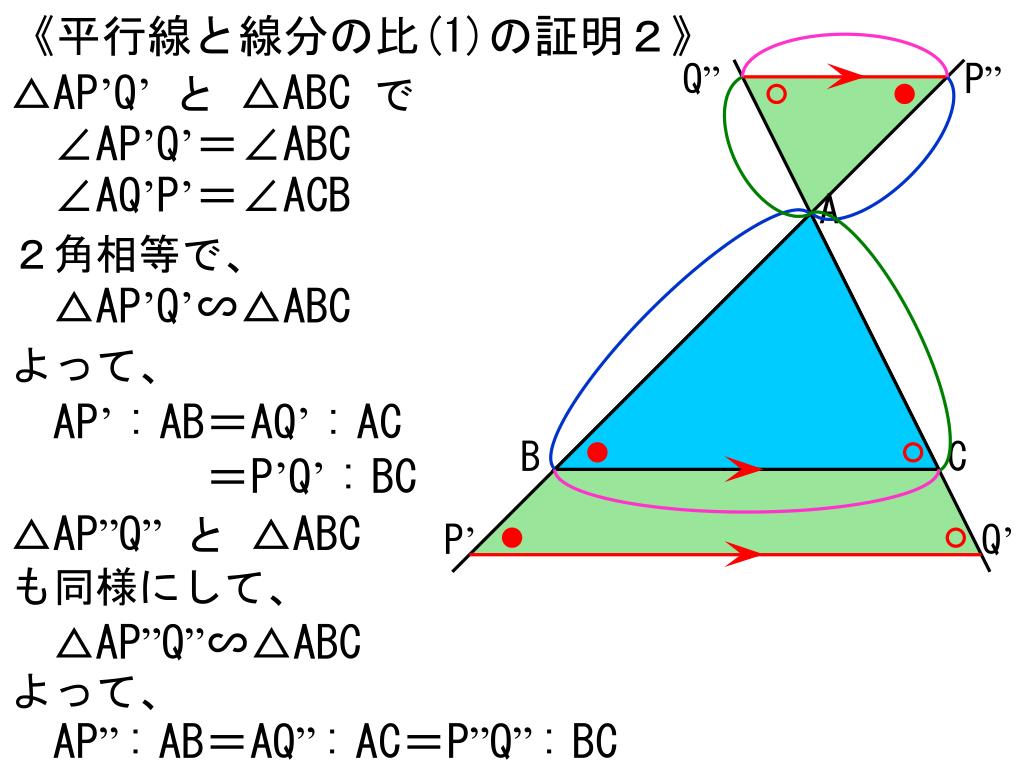



Ppt 5 図形と相似 Powerpoint Presentation Free Download Id



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1




線分比の移動の公式を教えてください よろしくお願いします Clear
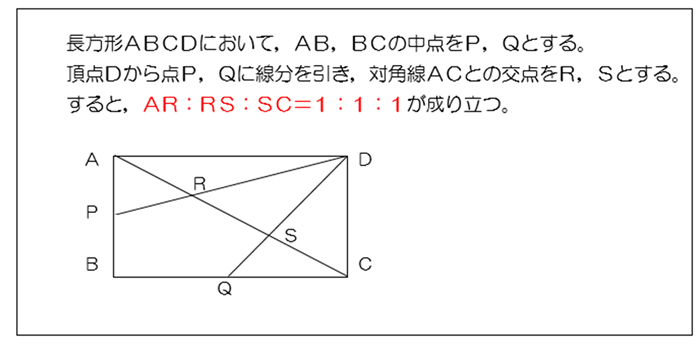



授業実践記録 数学 新しい 定理 とその活用 啓林館



平行線と線分の比 中学3年 数学クラブ
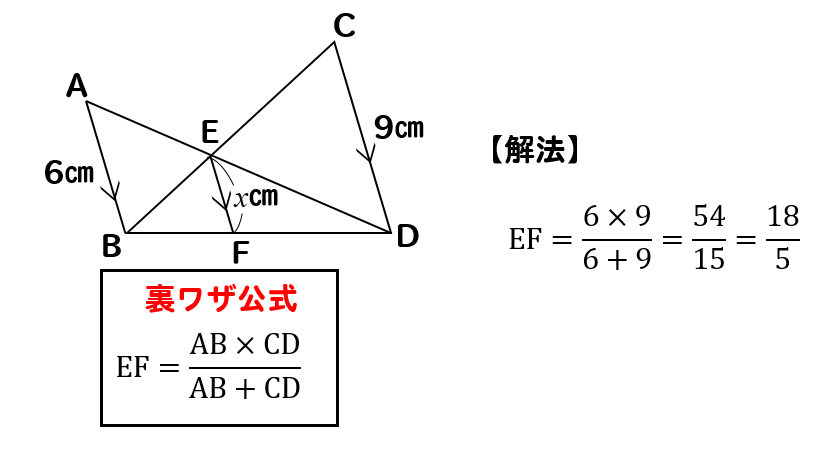



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ




相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に
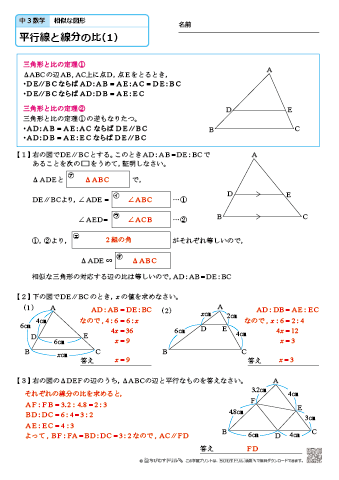



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




急ぎです Clear
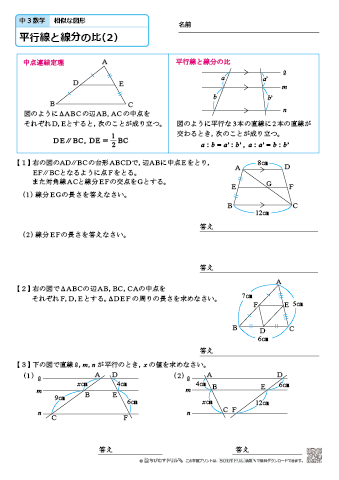



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
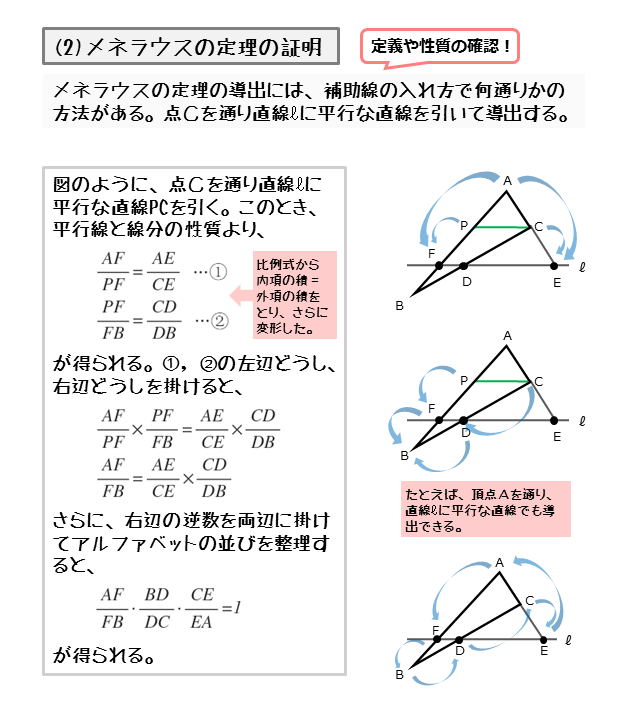



図形の性質 メネラウスの定理 チェバの定理について 日々是鍛錬 ひびこれたんれん
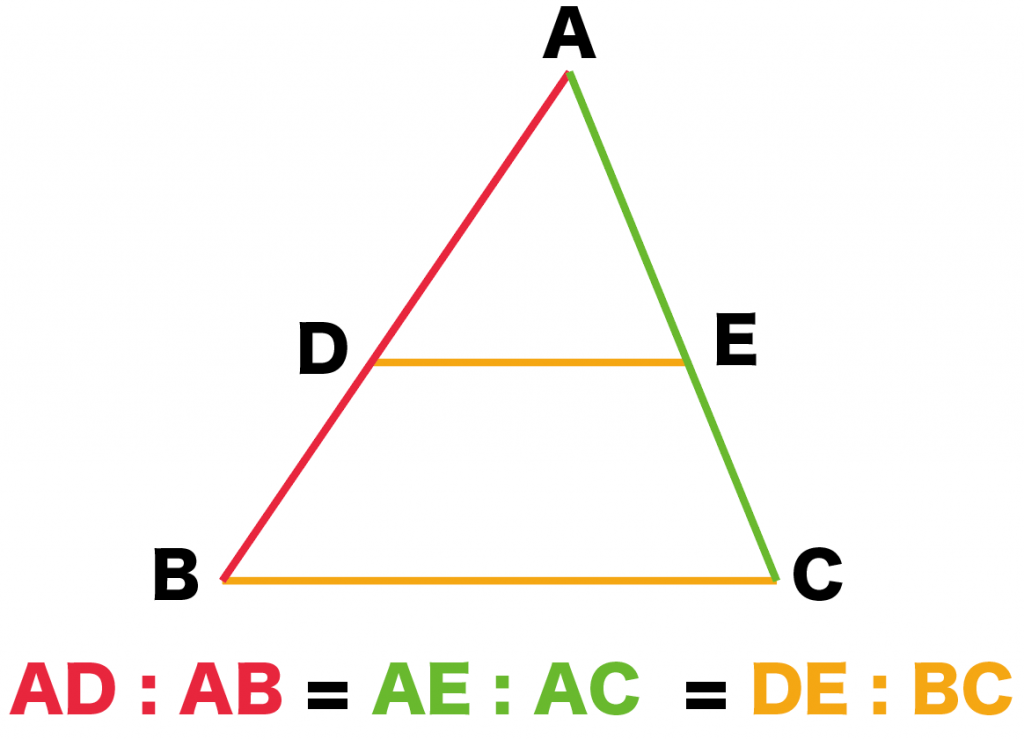



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく




角の2等分と線分の比 高校数学の無料オンライン学習サイトko Su




相似な図形 補助線を引いて考える相似の問題 中学生からの勉強質問 数学 進研ゼミ中学講座



Http Www Fdtext Com Dat Suub3 5zukei 2senbunhi Pdf
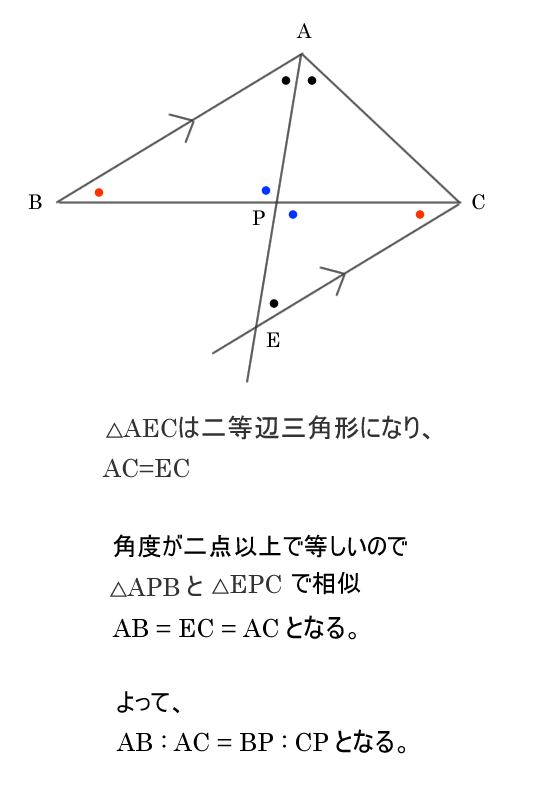



角の二等分線定理 証明 優技録



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典
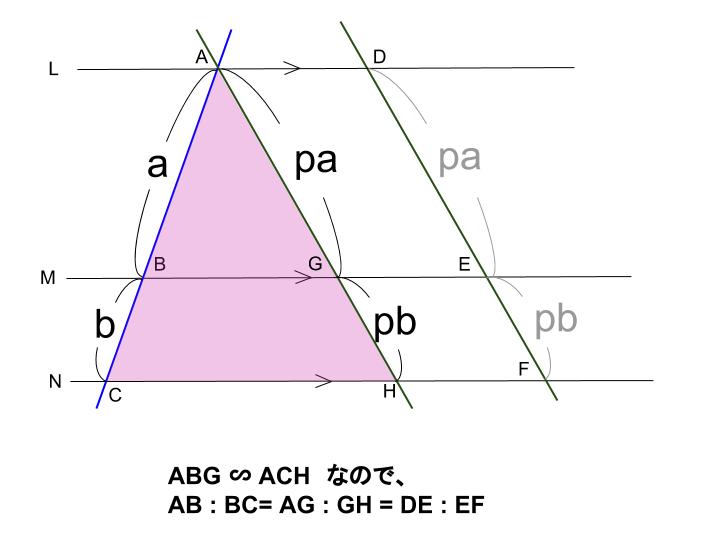



中学数学 平行線と線分の比 その1 中学数学の無料オンライン学習サイトchu Su




勉強しよう数学 10月 17



相似 平行 三角形と線分の比 勉強ナビゲーター
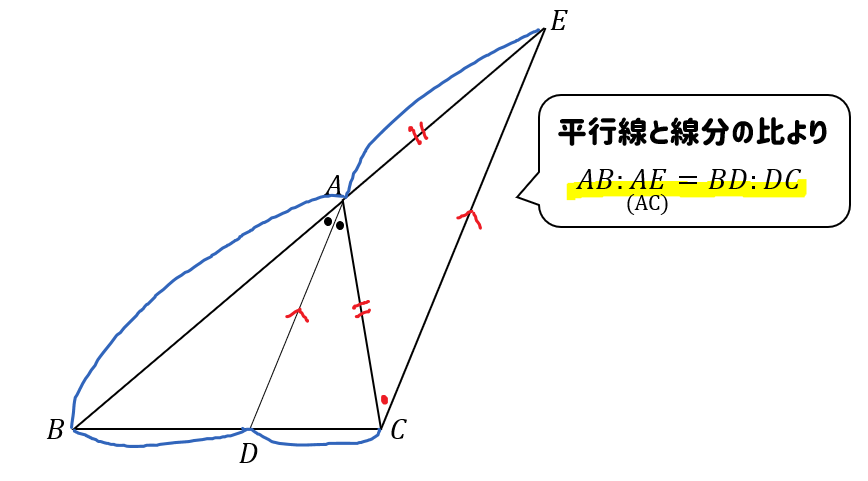



サクッと解説 角の二等分線と比の特徴となぜ について 数スタ




ねこ騙し数学




中3数学 平行線と比3 平行 線分比 映像授業のtry It トライイット
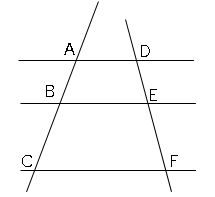



平行線と線分の比と中点連結定理 数学の要点まとめ 練習問題一覧



Studydoctor平行線と台形 中3数学 Studydoctor



2




数学 中3 51 平行線と線分の比 中点連結定理編 Youtube



Http Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Yaruki Suugaku Documents M3011 Pdf
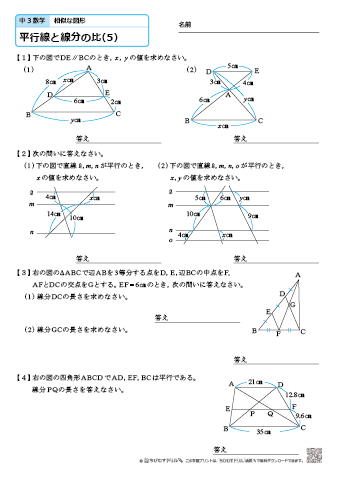



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



平行線と線分の比についてです この図形に平行線と線分の比があるのですが Yahoo 知恵袋




中3数学 相似の平行線と線分の比のポイントと定期テスト対策問題
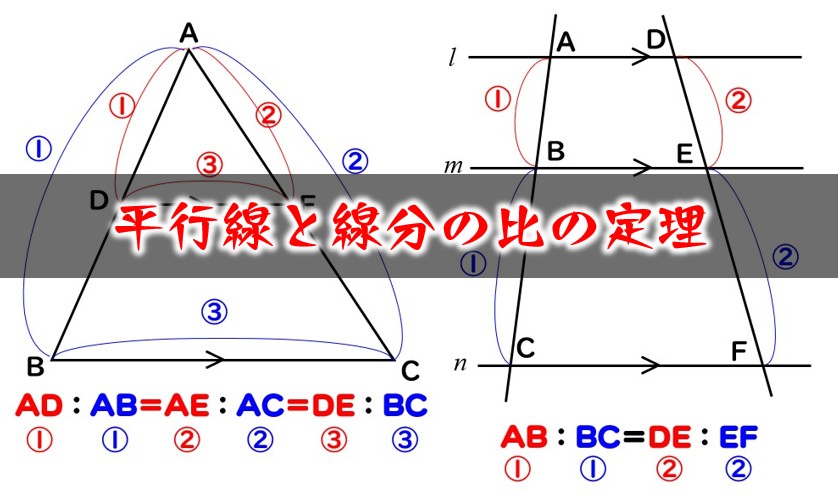



平行線と線分の比の定理 の問題の解き方 数学fun



0 件のコメント:
コメントを投稿